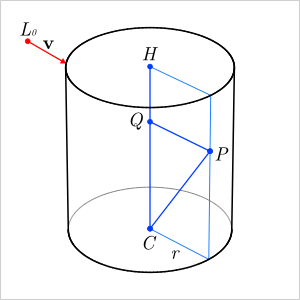
\( C \) = Point at the center of the base of the cylinder
\( H \) = Point at the center of the top of the cylinder
\( r \) = Cylinder radius
\( P \) = Point on the cylinder surface
\( L_{0} \) = Point on the line
\( \mathbf{v} \) = Vector that defines the line direction
Parametric equation of a point on the cylinder
A generic point on the cylinder satisfies the equation:
\[
\left\lVert P - C \right\rVert = \sqrt{\left\lVert Q - C \right\rVert^{2} + r^{2}}
\]
Both sides of the equation can be raised by the power of 2, to simplify the calculations.
\[
\left\lVert P - C \right\rVert^{2} = \left\lVert Q - C \right\rVert^{2} + r^{2}
\]
The vector \( \mathbf{h} \) represents the axis of the cylinder.
\[
\mathbf{h} = \left( H - C \right)
\qquad
\mathbf{\hat{h}} = \frac{\left( H - C \right)}{\left\lVert H - C \right\rVert}
\]
The segment \( \overline{CQ} \) can be expressed in terms of \( P \) as:
\[
\left\lVert Q - C \right\rVert = \left( P - C \right) \cdot \mathbf{\hat{h}}
\]
and substituted back.
\[
\left\lVert P - C \right\rVert^{2} - \left[ \left( P - C \right) \cdot \mathbf{\hat{h}} \right]^{2} = r^{2}
\]
Parametric equation of the line
A generic line defined by a point \( L_{0} \) and a direction vector \( \mathbf{v} \). It describes all the points along the line as a function of the parameter \( t \).
\[
L_{\left( t \right)} = L_{0} + t \mathbf{v}
\]
Intersections calculation
To calculate the intersection between cylinder and line, substitute the generic point \( P \) on the cylinder with a generic point on the line \( L_{(t)} \).
\[
\left\lVert L_{0} + t \mathbf{v} - C \right\rVert^{2} - \left[ \left( L_{0} + t \mathbf{v} - C \right) \cdot \mathbf{\hat{h}}\right]^{2} = r^{2}
\]
Define a vector \( \mathbf{w} \) equal to the difference of \( L_{0} \) and \( C \):
\[
\mathbf{w} = L_{0} - C
\]
and substitute back.
\[
\left\lVert t \mathbf{v} + \mathbf{w} \right\rVert^{2} - \left[ \left( t \mathbf{v} + \mathbf{w} \right) \cdot \mathbf{\hat{h}} \right]^{2} = r^{2}
\]
The length squared of a vector is equal to the dot product of the vector by itself.
\[
\left( t \mathbf{v} + \mathbf{w} \right) \cdot \left( t \mathbf{v} + \mathbf{w} \right) - \left[ \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right) t + \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right) \right]^{2} = r^{2}
\]
Expand the dot product and the power.
\[
\left( \mathbf{v} \cdot \mathbf{v} \right) t^{2} + 2 \left( \mathbf{v} \cdot \mathbf{w} \right) t + \left( \mathbf{w} \cdot \mathbf{w} \right) - \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right)^{2} t^{2} - 2 \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right) \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right) t - \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right)^{2} = r^{2}
\]
Group by the coefficients of \( t \).
\[
\left[ \left( \mathbf{v} \cdot \mathbf{v} \right) - \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right)^{2} \right] t^{2} + 2 \left[ \left( \mathbf{v} \cdot \mathbf{w} \right) - \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right) \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right) \right] t + \left( \mathbf{w} \cdot \mathbf{w} \right) - \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right)^{2} - r^{2} = 0
\]
Substitute the coefficients of \( t \) to obtain a simpler quadratic equation.
\[
\begin{cases}
a = \left( \mathbf{v} \cdot \mathbf{v} \right) - \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right)^{2} \\
b = 2 \left[ \left( \mathbf{v} \cdot \mathbf{w} \right) - \left( \mathbf{v} \cdot \mathbf{\hat{h}} \right) \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right) \right] \\
c = \left( \mathbf{w} \cdot \mathbf{w} \right) - \left( \mathbf{w} \cdot \mathbf{\hat{h}} \right)^{2} - r^{2}
\end{cases}
\]
Solve for \( t \).
\[
a t^{2} + b t + c = 0
\]
Intersection points
- if \( \left( b^{2} - 4 a c \right) > 0 \)
The distance between the cylinder axis \( \overline{CH} \) and the line \( L_{ \left( t \right) } \) is smaller than the cylinder radius \( r \). There are two intersections at:
\[
L_{int_{1,2}} = L_{0} + t_{1,2} \mathbf{v}
\qquad
t_{1,2} = \frac{ - b \pm \sqrt{ b^{2} - 4 a c } }{ 2 a }
\]
- if \( \left( b^{2} - 4 a c \right) = 0 \)
The distance between the cylinder axis \( \overline{CH} \) and the line \( L_{ \left( t \right) } \) is equal to the cylinder radius \( r \). The line \( L_{ \left( t \right) } \) is tangent to the cylinder.
- if \( \left| \mathbf{\hat{v}} \cdot \mathbf{\hat{h}} \right| \neq 1 \)
There is one intersection at:
\[
L_{int} = L_{0} + t \mathbf{v}
\qquad
t = - \frac{ b }{ 2 a }
\]
- if \( \left| \mathbf{\hat{v}} \cdot \mathbf{\hat{h}} \right| = 1 \)
The line \( L_{ \left( t \right) } \) lies on the cylinder surface. There are infinite intersections.
- if \( \left( b^{2} - 4 a c \right) < 0 \)
The distance between the cylinder axis \( \overline{CH} \) and the line \( L_{ \left( t \right) } \) is greater than the cylinder radius \( r \). There are no intersections.
If any intersections are found and the cylinder is not infinite, the projection of the intersections on the cylinder axis must be between the two extremities \( C \) and \( H \).
- if \( 0 \leq \left( L_{int} - C \right) \cdot \mathbf{h} \leq \left\lVert \mathbf{h} \right\rVert \)
The intersection is on the cylinder surface.
- if \( \left( L_{int} - C \right) \cdot \mathbf{h} < 0 \)
The intersection is below the base of the cylinder. Test the intersection with the base cap.
- if \( \left( L_{int} - C \right) \cdot \mathbf{h} > \left\lVert \mathbf{h} \right\rVert \)
The intersection is above the top of the cylinder. Test the intersection with the top cap.